My Research
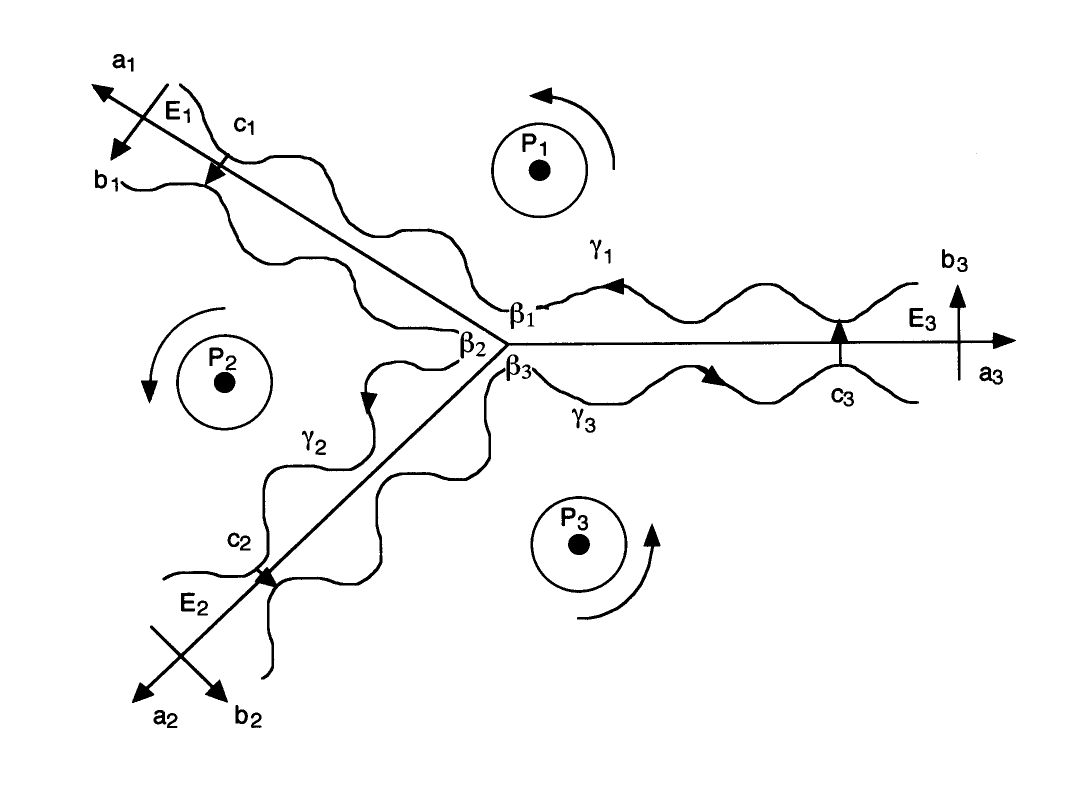
This is the intersection of a coplanar constant mean curvature
surface with its plane of symmetry; see papers by N. Korevaar,
R. Kusner, and myself.
My research lies at the intersection of geometry and
analysis. For instance, you might ask how much land you
can enclose with 100 miles of fencing; this is the classical
isoperimetric problem, which people have studied for
over
2000 years. If you have a very large, flat field, the
optimal shape is the first one you'd guess: a circle. However,
the answer changes if, say, the land is a narrow strip
between two forests, or if there's a river running through
the field, or if the land isn't flat. (Is it better to
surround the top of a hill or the pass between two peaks?)
The best shape will
satisfy a differential equation, and the solutions to this
equation depend very much on the geometry of the land. Problems
like that of finding isoperimetric regions form a
rich area of study, with connections to other areas of mathematics
such as function theory, probability, and topology, and even some
applications.
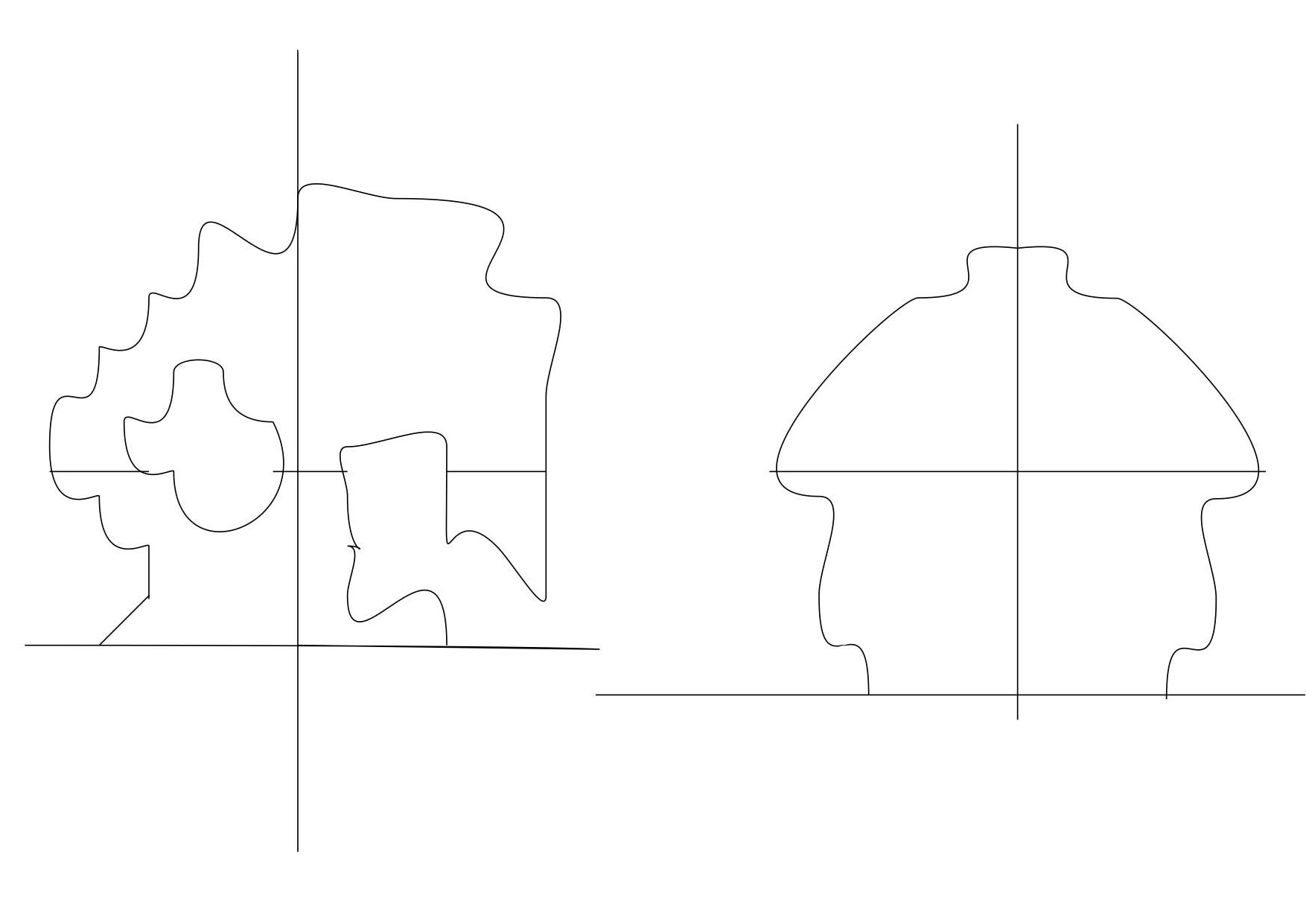
This picture illustrates Schwarz symmetrization; see my paper
about eigenvalues of domains in wedges.
Coauthors:
Tom
Carroll, UCC, Ireland;
Andrejs Treibergs,
U. Utah, US; Nick Korevaar,
U. Utah, US; Rob Kusner,
U. Mass, US; John
Sullivan, TU Berlin, Germany;
Karsten
Grosse-Brauckmann, TU Darmstadt, Germany
Papers (preprint versions available on
the the
arXiv):
- Monotonicity of the first
Dirichlet eigenvalue of the Laplacian on manifolds of nonpositive
curvature, (joint with T. Carroll) to appear in the Indiana U.
Math. J.
- A reverse Holder inequality
for extremal Sobolev functions. (joint with T. Carroll) Potential
Analysis 42 (2015), 283-292.
- A numerical investigation of level sets of
extremal Sobolev functions (joint with S. Juhnke), to appear in Involve.
- An isoperimetric inequality for
extremal Sobolev functions. (joint with T. Carroll), RIMS Kokyuroku
Bessatsu B43 (2013), 1-16.
- Two isoperimetric
inequalities for the Sobolev constant. (joint with T. Carroll),
Z. Angew. Math. Phys. 63 (2012), 855-863.
- Isoperimetric
inequalities and variations on Schwarz's lemma.
(joint with T. Carroll), preprint which has mostly been subsumed by later papers.
- Interpolating
between torsional rigidity and principal frequency. (joint with
T. Carroll) J. Math. Anal. Appl. 379 (2011), 818-826.
-
Eigenvalues of Euclidean wedge domains in higher
dimensions. Calc. Var. and PDE. 42 (2011), 93-106.
- Coplanar
k-unduloids are nondegenerate (joint with K. Grosse-Brauckmann,
N. Korevaar, R. Kusner, and J. Sullivan) Int. Math. Res. Not.
2009, 3391-3416.
- A Payne-Weinberger eigenvalue estimate for wedge domains on
spheres (joint with A. Treibergs) Proc. Amer. Math. Soc.
137 (2009), 2299-2309.
- A caputre problem in Brownian motion and eigenvalues of
spherical domains (joint with A. Treibergs) Trans. Amer.
Math. Soc. 361 (2009) 391-405.
- On
the nondegeneracy of constant mean curvature surfaces (joint with
N. Korevaar and R. Kusner) Geom. Funct. Anal. 16 (2006),
891-923.
- An
end-to-end gluing construction for metrics of constant positive scalar
curvature. Indiana U. Math. J. 52 (2003), 703-726.
- An end-to-end gluing construction
for surfaces of constant mean curvature PhD dissertation,
U. Washington, 2001.
I've also written some miscellaneous notes related
to my research, which you can read (if you're curious and
somewhat masochistic) by clicking here.
Jesse Ratzkin
jesse.ratzkin@uct.ac.za
back to Jesse's home page


